Einheitsvektoren
Ein Einheitsvektor ist ein Vektor der Länge 1.
Wie bekommt man einen solchen Einheitsvektor?
Man teilt den Vektor einfach durch seine Länge! Einheitsvektoren werden zumeist
mit dem Index 0 als solche gekennzeichnet. Wenn also
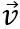 ein Vektor und
ein Vektor und
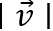 seine Länge ist, so ist
seine Länge ist, so ist 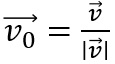 der zugehörige Einheitsvektor.
der zugehörige Einheitsvektor.
Wozu braucht man Einheitsvektoren?
Wie wir gleich sehen werden sind Einheitsvektoren Bestandteil der Hesse'schen Normalenform
der Ebenengleichung.
Rechenbeispiel
Bilde zu 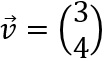 einen Einheitsvektor.
einen Einheitsvektor.
Lösung
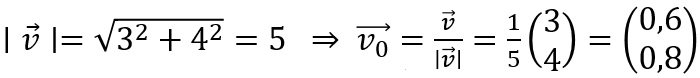

Wenn man in der Normalenform einer Ebenengleichung statt dem Normalenvektor einen Einheitsnormalenvektor (also einen Normalenvektor der Länge 1) verwendet, so erhält man die Hesse'sche Normalenform (HNF):
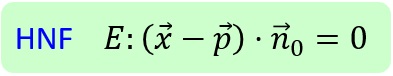
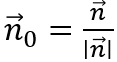 ein
Einheitsnormalenvektor.
ein
Einheitsnormalenvektor.Wofür braucht man dies?
Unter Verwendung der HNF kann später der Abstand eines Punktes zu einer Ebene sehr bequem (durch Einsetzen) berechnet werden!
Rechenbeispiel
Die Ebene E sei gegeben durch E: x1+2x2-2x3=4.
Wie lautet die entsprechende Hesse'sche Normalen Form der Ebene E?
Lösung
In E: x1+2x2-2x3=4 liest man zunächst den Normalenvektor mit
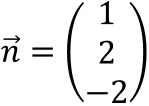 ab.
Mit
ab.
Mit 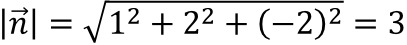 folgt
folgt 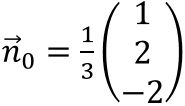 .
.Nun suchen wir uns einen beliebigen Punkt P, der in E liegt, den wir dann als Stützvektor verwenden können. Dazu setzen wir zwei beliebige Koordinaten der Ebenengleichung gleich Null und berechnen die dritte Koordinate. Beispielsweise setzen wir x1=x2=0 und erhalten x3=-2.
Somit liegt P(0|0|-2) in E und wir erhalten folgendes
Ergebnis: Die HNF für E lautet
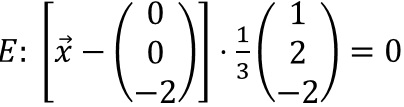 .
.HNF in Koordinatenschreibweise
Es gibt auch eine Koordinatenschreibweise der HNF. Diese verwendet man sinnvollerweise dann, wenn die Ebenengleichung in Koordinatenform vorliegt. Dabei formt man die Koordinatengleichung so um, dass man zunächst alles auf die linke Seite bringt, so dass auf der rechten Seite der Gleichung eine Null steht. Anschließend teilt man die linke Seite durch die Länge des Normalenvektors. Wenn E durch E:ax1+bx2+cx3=d gegeben ist, sieht das formal dann so aus:
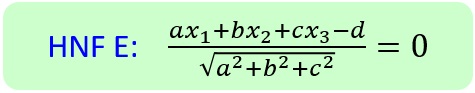
Rechenbeispiel
Wandle E: x1+2x2-2x3=4 um in die Hesse‘sche Normalenform (Koordinatenschreibweise).
Lösung
Mit
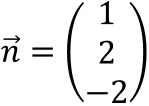 folgt
folgt 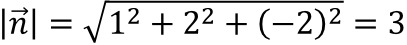 .
Daraus erhalten wir direkt die HNF.
.
Daraus erhalten wir direkt die HNF.Ergebnis:
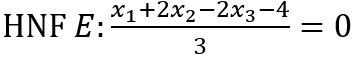 .
.
| Downloads |
PowerPoint